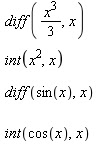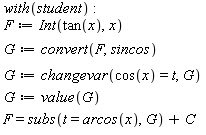Benemérita Universidad Autónoma de Puebla

Facultad de Ciencias de la Computación

Cálculo Integral

PRÁCTICA 6 INTEGRACIÓN POR PARTES

Se basa en la fórmula de derivación de un producto. Si u y v son dos funciones con derivadas continuas se tiene

Ejemplo

Calcular

En este caso la elección obvia es ln(x) = u(x). Los cálculos suelen organizarse de la siguiente manera

 

Ejercicios

Para cada función:
Elegir las variable u y dv.
Explicar el porqué de su decisión.
Obtener la Integral usando la forma para la integración por partes en Maple.
¿Fue correcta su elección de las variables u y dv? ¿Porqué?

Escribir brevemente los problemas que se le presentaron durante la práctica y explicar como es que los solucionó.
Enviar la práctica en horario de 15 a 17hrs a la dirección de correo electrónico liliamn@cs.buap.mx

Práctica 4 Arquitectura

Benemérita Universidad Autónoma de Puebla

Facultad de Ciencias de la Computación

Arquitectura de Computadoras

Práctica 4

Objetivo: Realizar un programa en lenguaje ensamblador que opere un crucero de dos semáforos.



Especificaciones:

 El tiempo de duración será:

• En rojo: tres veces el tiempo que tarde el semáforo en amarillo

• En verde: dos veces el tiempo que tarde el semáforo en amarillo

• En amarillo: el tiempo que Ud. elija para un ciclo del semáforo.

 Cuando un semáforo esté en el ciclo verde - amarillo, el otro estará en rojo y viceversa.

 Una vez terminado y compilado el programa, se simulará en proteus, y se comprobará que los resultados obtenidos correspondan a lo que se pidió.

 Presente un informe del desarrollo de la práctica que contenga:

 Portada con nombres de todos los integrantes del equipo

 Procedimiento empleado

 Programas

 Figuras

 Consultas

 Justificación de los resultados obtenidos.

 Conclusiones.

 Enviar a liliamn@cs.buap.mx el día 28 de febrero de 2011.

Práctica 5 Cálculo Integral

Métodos de integración


Bajo la expresión “Métodos de integración” se engloban una serie de técnicas diseñadas con el fin de obtener el conjunto de primitivas (o integral indefinida) de una función dada. Desde un punto de vista estricto se trata de “antiderivar” una función pero el uso de la palabra “integración” está justificado por la importancia que las primitivas juegan a través de la Regla de Barrow. A diferencia de la derivación, donde basta conocer unas pocas reglas elementales, la integración dista mucho de ser una tarea mecánica. El alumno no debe perder de vista que el cálculo de primitivas es un auténtico arte en el que no hay reglas fijas y sí una gran dosis de intuición e imaginación, desarrollable sólo a través de la práctica y el ejercicio constante. A continuación comentaremos los métodos de integración de aplicación más general, enunciando brevemente su fundamento teórico. Cada método se ilustrará con un ejemplo completamente desarrollado que, además, servirá para introducir las técnicas de trabajo básicas de Maple.
El primer conjunto de reglas de integración se obtiene sin más que “leer” de derecha a izquierda las expresiones que proporcionan las derivadas de las funciones elementales. La pantalla de Maple que aparece a continuación ilustra, sobre dos casos simples, cómo operan los comandos diff e int para el cálculo de derivadas e integrales respectivamente.

Nótese que los comandos diff e int operan esencialmente como inverso uno del otro. No obstante hay que tener presente que int genera una única primitiva, es decir no añade por si mismo la constante de integración.
Operando como se ha indicado anteriormente se construye la siguiente tabla que recoge las integrales conocidas como inmediatas:

Naturalmente, en la mayor parte de los casos la integral que se debe calcular no es inmediata. Los siguientes métodos de integración tratan, precisamente, de transformar y/o descomponer la función integrando en expresiones fácilmente reconocibles como integrales inmediatas.
1. INTEGRACIÓN POR DESCOMPOSICIÓN: Es consecuencia directa de la linealidad de la integral

Realizar en maple de la siguiente forma:

Nótese, en la primera línea, la utilización del comando Int que proporciona una expresión no evaluada de la integral. A continuación hemos utilizado el comando expand para realizar la descomposición de la integral. En la última expresión se utiliza value para escribir explícitamente el valor de cada una de las integrales que habíamos obtenido en la línea anterior.

Ejercicios
Realizar las siguientes integrales por descomposición

2.INTEGRACIÓN POR SUSTITUCIÓN (CAMBIO DE VARIABLE) Si f y la derivada de j son continuas entonces

Maple implementa el método de sustitución por medio del comando changevar. A continuación se muestra cómo se realizan los cálculos por medio de este programa. El primer comando carga el paquete student en el que se encuentra definido changevar. El segundo define la integral F, en la cual estamos interesados. A continuación introducimos una variable temporal G en la que iremos guardando las manipulaciones que efectuemos a partir de la integral original. De entrada usamos el comando convert, con su segundo argumento igual a sincos, para reescribir la expresión original en términos de senos y cosenos. En la cuarta expresión efectuamos el cambio de variable, lo que nos proporciona una integral inmediata que es evaluada, usando value, en la quinta instrucción. La última línea presenta el resultado obtenido al efectuar la integración.

Ejercicios

Después de realizar los ejercicios, escribe las dificultades que se te presentaron y la forma de solucionarlas.
Envía tu práctica.